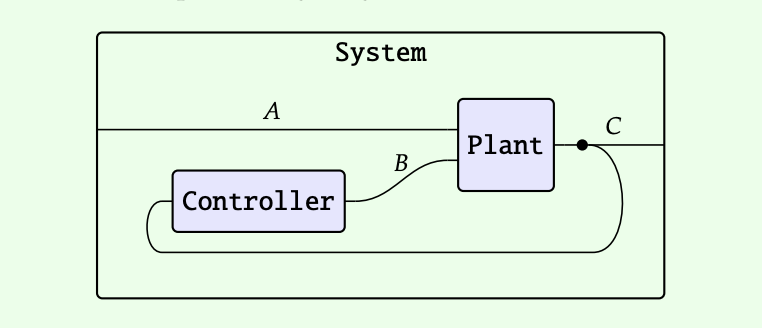
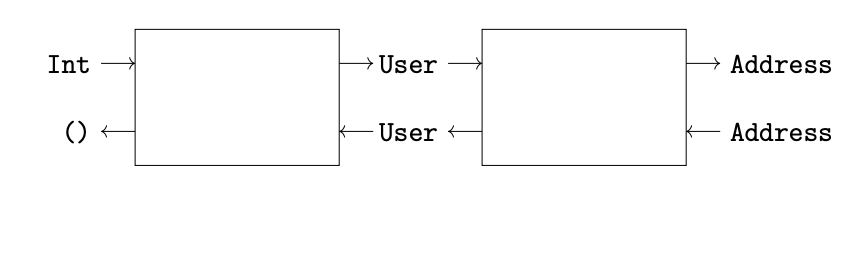
Table of Contents:

1. Introduction

   1. Overview
   2. Caveats & Goals
2. Background

   1. Boxed View
   2. Horizontal View
3. More Optics in Poly

   1. Prism
   2. Optional
   3. Traversal
   4. Limitations

Introduction

Background

Notoriously, lenses have been independently discovered many times. A diversity of notations and illustrations abound, yet arguably only one of these "optical" traditions has seen adoption in industrial practices: lenses and prisms, etc. For example, libraries such as Scala's Monocle and Haskell's lens provide functional getters and setters which have proved useful for manipulating complex data structures. As research into optics continues to bubble over with new insights, we have incentive to compare some of these diverse representations.

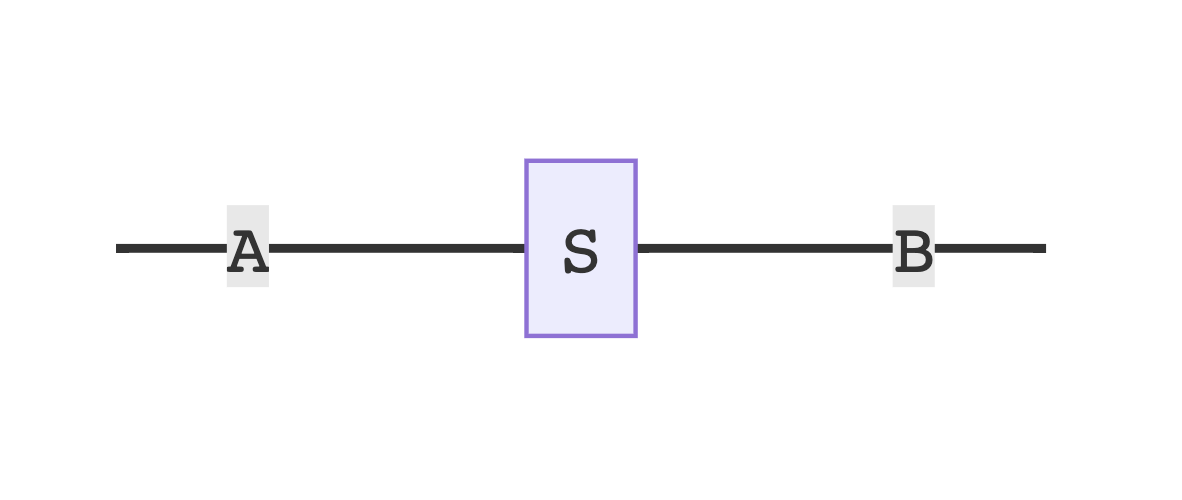
Boxed View

The monomial lenses described in Niu and Spivak are illustrated using what could be called a "boxed" view. For example, recall from a previous post the examples of a monomial state box, and wiring diagram within which it can be nested:

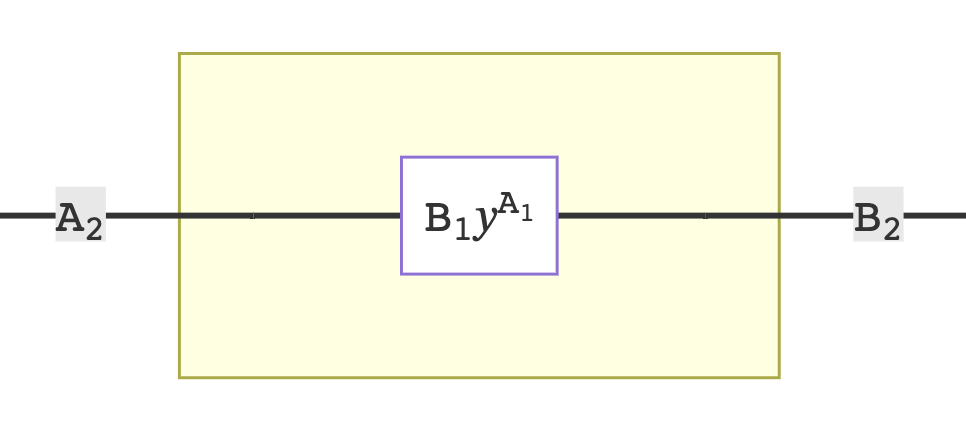
We could interpret the depictions above as taking a profile view, or a frontal view, or a plan view. In any case, the principle of lens composition is represented as the nesting of state lenses within wrapper interfaces. A wrapper interface may itself be wrapped, just as there is no limit to the infinite well of possible nestings inside it.

The diagrams are sometimes labeled with state positions S and interace positions I. In our example, they are also labeled with state positions S, but interface positions are lebeled B. This is done in order to suggest an identity with Moore machines and Mealy machines, or more generally a dynamic function (i.e., a function A => B, with an associated state S).

Horizontal View

If you've run across lenses via functional programaming, you may have see a "horizontal" representation. Rather than representing lens composition as nested boxes, we instead see how the horizontal composition suggests a post-compose operation analogous to function composition:

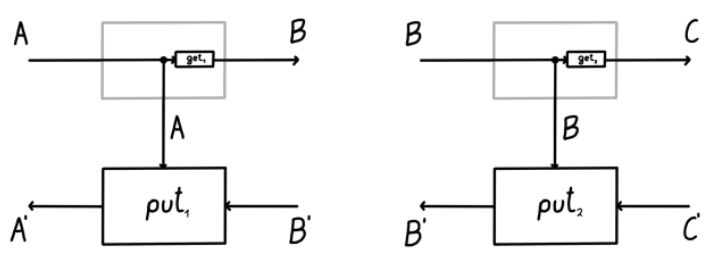
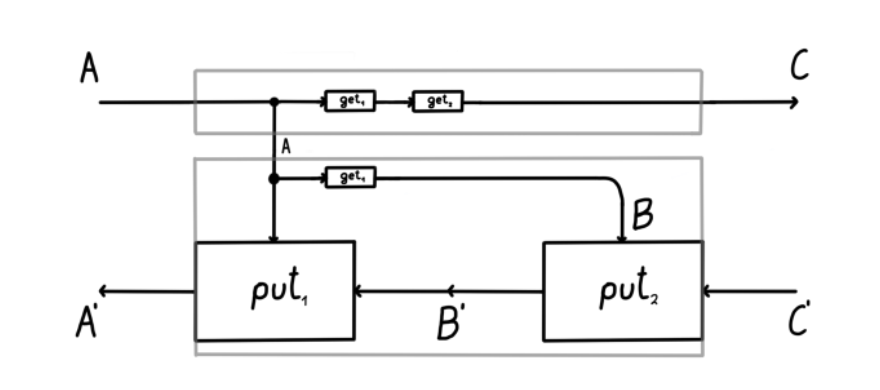
Horizontal representations can appear in various degrees of abstraction. The "horizontal" example above shows lens composition in full detail. A slightly different notation than in Spivak's presentation, the most simple version is perhaps Monocle's Lens[S, A], where S is the only state type, and A the only input/output type. But in the example above, we see that each lens has four types, in which, despite the relabeling, we might recognize the Lens type from Haskell's lens library: type Lens s t a b. In the Lens type, in contrast with Spivak's "boxed" presentation, not only do we add a second state type T, but we also swap input and output labels A and B:

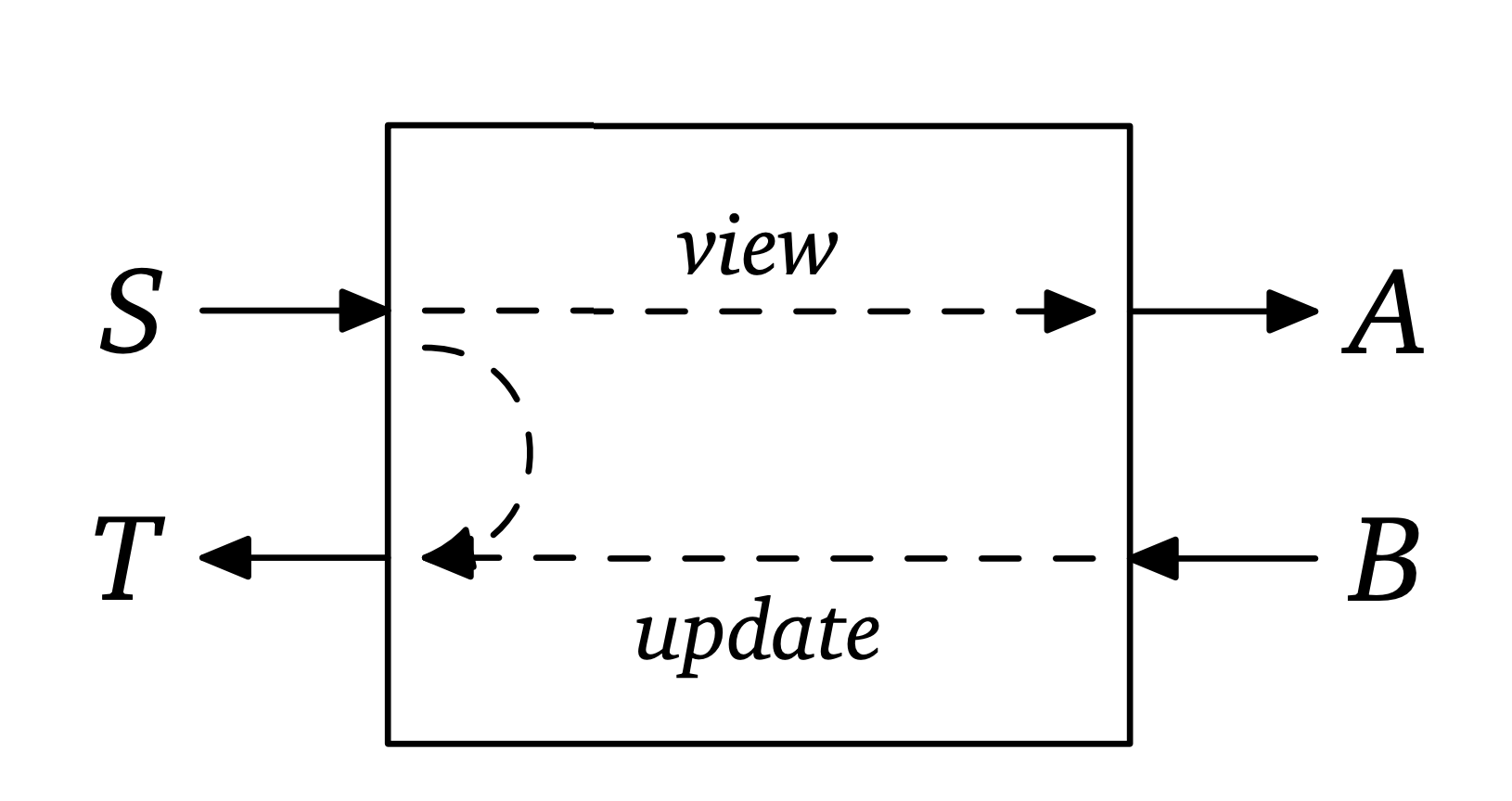
Under the hood, Monocle follows the lens library's naming scheme, and explains in a comment the role of each type. Let's compare the definition provided by Spivak with this other, somewhat standardized, definition:

/* A "view" function */
def φ: S => B

/* An "update" function */
def `φ#`: (S, A) => S

/* i.e. from an `S`, we can extract an `A` */
def get: S => A

/* i.e. if we replace an `A` by a `B` in an `S`, we obtain a `T` */
def set: (B, S) => T

Prism

It is known that morphisms in Poly can represent prisms. Can we model them in Scala using our PolyMap representation? According to Monocle, a Prism "can be seen as a pair of functions: getOrModify: S => Either[T, A] and reverseGet: B => T." So, yes, if we squint, we can see a readout function S => B and an update function (S, A) => S that discards the current state. Our examples are "mealified" so they may be run, and will use Option instead of Either, but the same principles of prism composition apply, and in both cases a flatMap can be used to implement the composition:

extension [S, A, B, Y] (p: PolyMap[Store[Option[S], _], Interface[A, Option[B], _], Y])
  def andThen(
    w: PolyMap[Interface[A, B, _], Interface[A, A => Option[B], _], Y]
  ): PolyMap[PolyMap[Store[Option[S], _], Interface[A, B, _], _], Interface[A, A => Option[B], _], Y] =
    new PolyMap[PolyMap[Store[Option[S], _], Interface[A, B, _], _], Interface[A, A => Option[B], _], Y]:
      def φ: Phi[PolyMap[Store[Option[S], _], Interface[A, B, _], _], Interface[A, A => Option[B], _], Y] =
        s => a => p.φ(s).flatMap(b => w.φ(b)(a))
      def `φ#`: PhiSharp[PolyMap[Store[Option[S], _], Interface[A, B, _], _], Interface[A, A => Option[B], _], Y] =
        (s, a) => p.φ(s).flatMap(b => p.`φ#`(s, w.`φ#`(b, a)))

Optional

When a prism doesn't discard it's current state on update, then we get a more general type, an Optional. Monocle again describes a pair of functions: getOrModify: S => Either[T, A] and replace: (B, S) => T. Thus, we can reuse for optionals the same composition function that we implemented for prisms, allowing us to form a Mealy machine by composing morphisms, just as we would with a lens:

val m: Moore[Store[Option[Boolean], _] ~> Interface[Int, Option[Int], _]] =
  Moore(
    // initialize with `true`
    Some(true),
    // if non-empty, map to int
    s => s.map(b => if b then 1 else 0),
    // if we've seen `i > 1` then update with `None`
    (s, i) => if i > 1 then None else s.map(b => !b)
  )

val w: Wiring[Interface[Int, Int, _] ~> Interface[Int, Int => Option[Int], _]] =
  Wiring(
    // double if we've seen j > 1
    i => j => if j > 1 then Some(j + j) else Some(i),
    // identity
    (i1, i2) => i2
  )

val machine =
  m.andThen(w).asMealy

val result: List[Option[Int]] =
  List(1, 2, 3).mapAccumulate(machine.init)(machine.run)._2
// List(Some(1), Some(4), None)

Traversal

Traversals are often presented along with lenses, prisms, and optionals: "It allows you to traverse over a structure and change out its contents with monadic or Applicative side-effects" (lens). Such a constraint will be no obstacle to composition, given that our prism and optional compositions were implemented using flatMap.

val m: Mealy[Store[List[Int], _] ~> Interface[Int, Int => List[Long], _]] =
  Mealy(
    List(10, 20, 30),
    s => _ => s.map(_.toLong),
    (s, i) => s.map(v => i * v)
  )

val obtained: List[List[Long]] =
  List(1, 2, 3).mapAccumulate(m.init)(m.run)._2
// List(List(10, 20, 30), List(10, 20, 30), List(20, 40, 60))

Limitations

What else lies within the morphisms of Poly? We've seen some familiar optics fall out from our investigations, so how far can we get with the "boxed" illustration style of Niu and Spivak?

So far, we've juxtaposed, on one hand, morphisms between monomials in Poly, and on the other hand, a family of optics familiar to programmers:

1. We compared the notations, and saw that familiar optics can be implemented as natural transformations between polynomial functors and their composition.
2. We compared the illustrations, observing that Niu and Spivak's "boxed" style is simplified and more abstract, whereas the standard "horizontal" style is not only more prevalent but also more detailed.

The simplicity of the "boxed" illustration becomes worth sacrificing once we need a more detailed "horizontal" representation. The "boxed" style of illustration abstracts away the dependence of the update function on the "old state", and will thus fail to illustrate strength. Therefore, we'll see the "boxed" illustration excel at representing tensor products of monomial lenses, and try out the "horizontal" illustration when representing, e.g., cartesian products of polynomial functors.

Finally, I'm not sure what is more surpising: that so many familiar optics are readily visible in the polynomial representation of lenses? Or, that Tambara Modules seem to be more closely within reach than Profunctor Optics? Stay tuned to see if anything comes of this mystery.