Dynamical Systems, in Series and in Parallel
What's a dependent dynamical system? With Scala 3's support for ADTs and match types, and some guidance from Niu and Spivak, we can use polynomial functors to model complex state machines in a type-safe and compositional way.
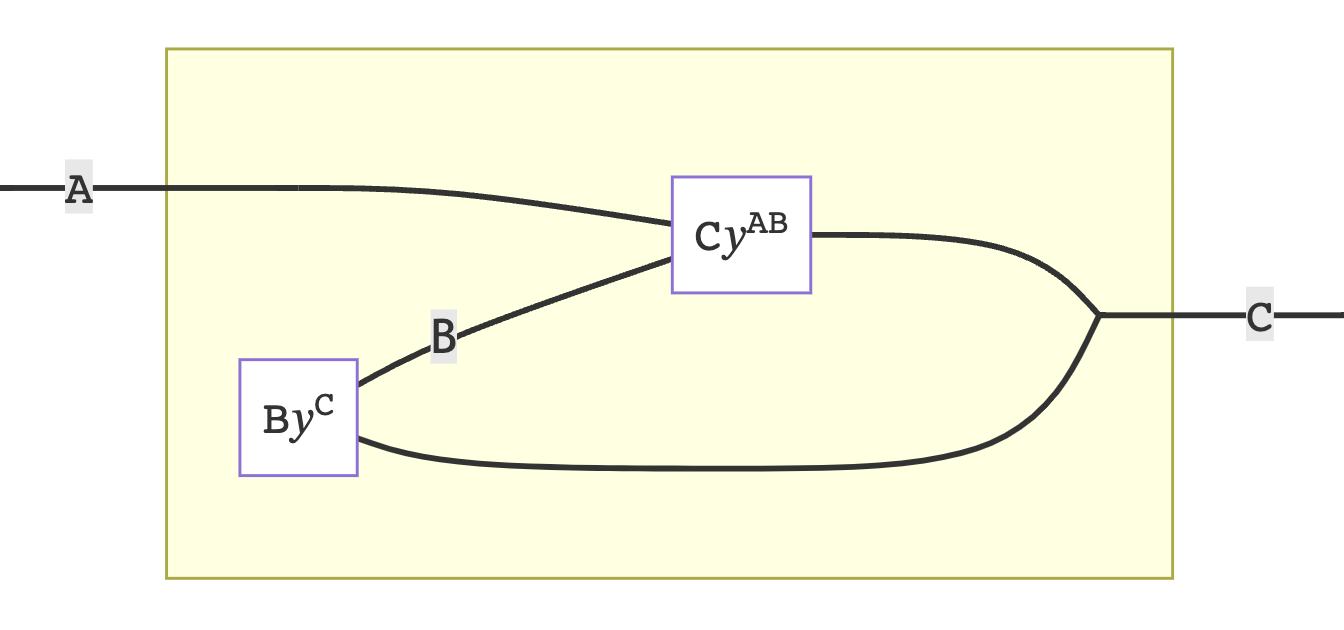
Table of Contents:
-
Introduction
-
Tensor Product
-
Swap, Project, Discard, Duplicate
Introduction
Overview
We'll use tensor products, aliased by the ⊗ symbol, to wire up multiple lenses in a single interaction pattern.
Caveats and Goals
The usual caveats apply: I'm not an expert in Poly, I'm a Scala developer, and a math enthusiast attempting to interpret aspects of Poly into Scala, a simply-typed programming language. As such, criticism is appreciated.
My goals here are:
- to explore the utility of a "lawless" implementation of a Poly in Scala, using ADTs and match types instead of fully dependent types
- to share and get feedback about this method of representing Poly, and the finite state machines they can model
- to try to make a Scala artifact out of the poly book, in the form of a library that can be improved over time
Tensor Product
Among the many interesting products in Poly, the tensor product, or ⊗, provides a way to combine two polynomial functors into one. Ultimately, this allows us to interpret morphisms between such tensored functors as representing multiple state machines running in a single system. We can take as prototypical the examples of a monomial state lens and a monomial wiring diagram:
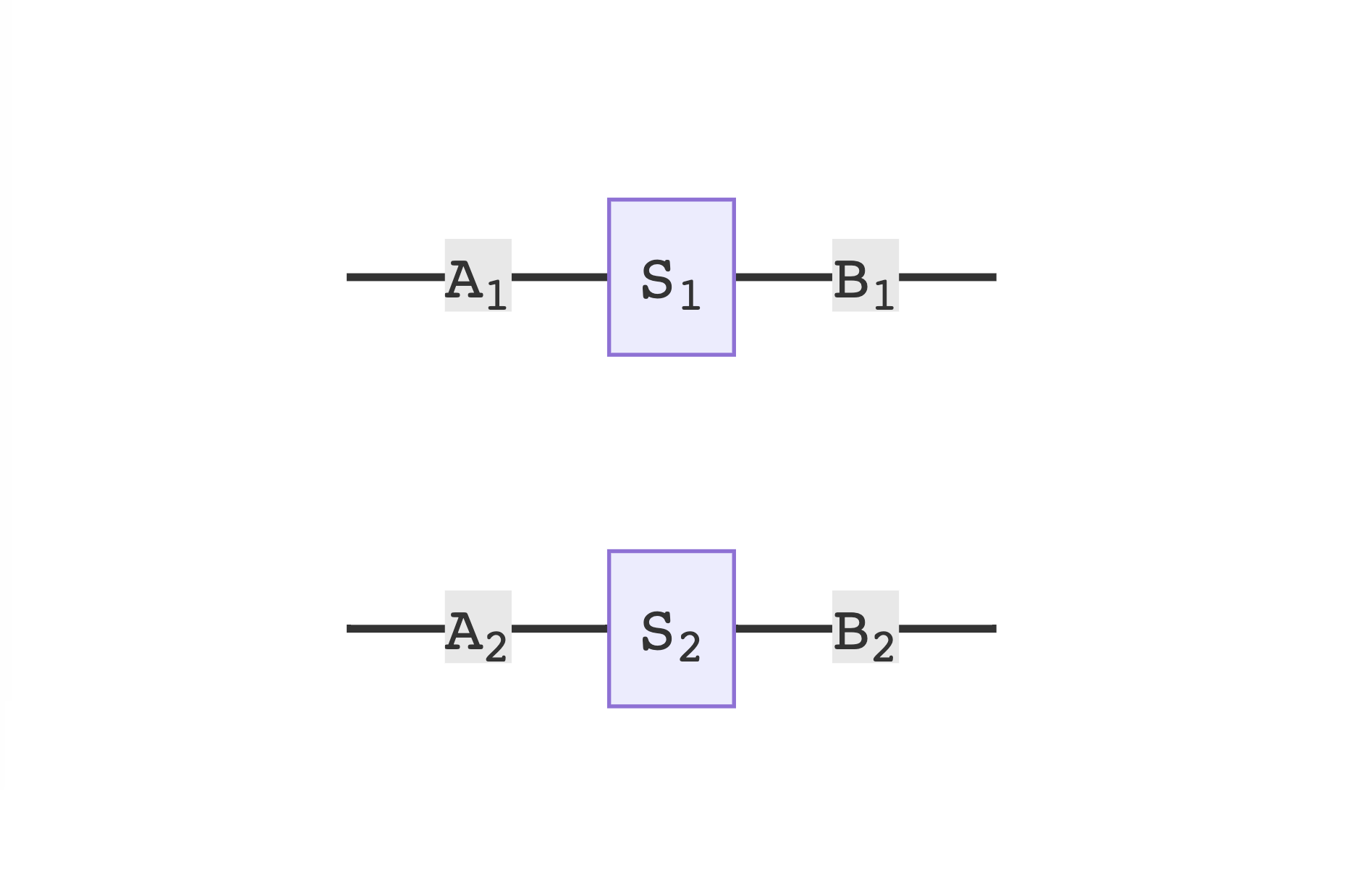
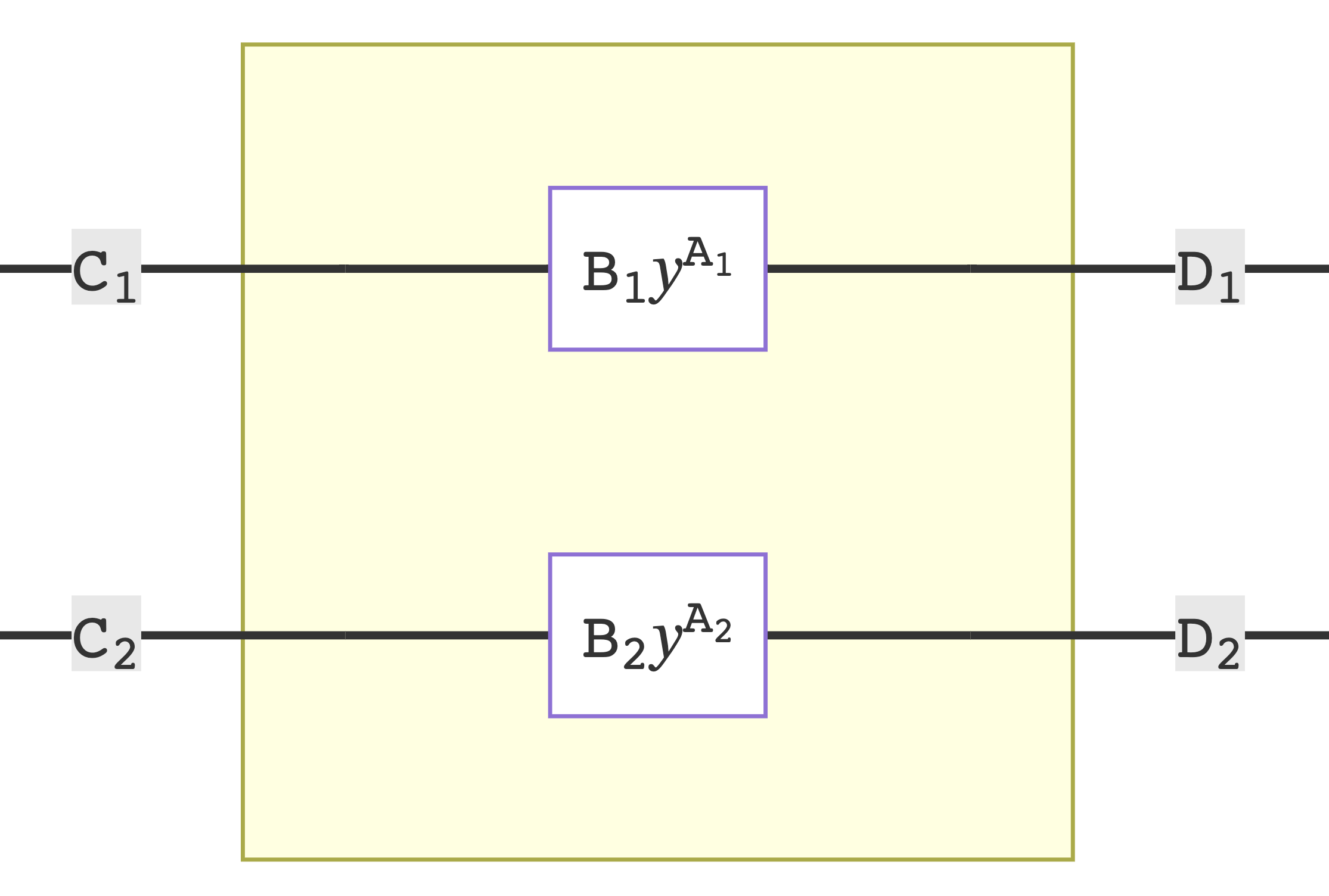
To describe the mechanism of tensoring, I might suggest "systematic tupling": of objects, of morphisms, of positions, of directions, of inputs, of outputs. It is covered in day 3 of the Polynomial Functors course, in this video, and a larger example is described here. For the purpose of our explorations, we can use match types to accomplish this in Scala 3:
case (Store[s1, Y], Store[s2, Y]) =>
Store[(s1, s2), Y]
case (Interface[a1, b1, Y], Interface[a2, b2, Y]) =>
Interface[(a1, a2), (b1, b2), Y]
case (PolyMap[o, p, Y], PolyMap[q, r, Y]) =>
PolyMap[DayConvolution[o, q, _], DayConvolution[p, r, _], Y]We can see at a glance that the products formed are symmetric monoidal. But, in terms of state machines, what is the effect of tensoring two state lenses into a single system?
Parallel Systems
When tensored functors are used to define a lens, the result is parallelism. For example, we can tensor together two "integer doublers" and run them as one. In the following example, a Moore machine is used, rather than a Mealy machine, simply in order to reveal the implementation of the run function, but a Mealy machine could just as easily be used:
val m1: Moore[Store[Boolean, _] ~> Interface[Int, Int => Int, _]] =
Moore(false, s => i => i + i, (s, i) => s)
val m2: Moore[Store[Boolean, _] ~> Interface[Int, Int => Int, _]] =
Moore(false, s => i => i + i, (s, i) => s)
val m3: Moore[
(Store[Boolean, _] ⊗ Store[Boolean, _]) ~>
(Interface[Int, Int => Int, _] ⊗ Interface[Int, Int => Int, _])
] =
m1 ⊗ m2
val l: List[(Int, Int)] =
List((1, 11), (2, 22), (3, 33)).mapAccumulate(m3.init)(
(s, a) => (m3.update(s, a), (m3.readout(s)._1(a._1), m3.readout(s)._2(a._2)))
)._2
// List((2, 22), (4, 44), (6, 66))Serial Systems
Tensored lenses can also be used to define serial systems. By composing a tensored state lens with a wrapper interface, a parallel system can be wired in series:
val m: Moore[
(Store[Boolean, _] ⊗ Store[Boolean, _]) ~>
(Interface[Int, Long, _] ⊗ Interface[Long, String, _])
] =
(Moore(
false,
s => if s then 1L else 0L,
(s, i) => if i > 1 then true else false
) ⊗
Moore(
false,
s => if s then "true" else "false",
(s, i) => if i > 0L then true else false)
)
val w: Wiring[
(Interface[Int, Long, _] ⊗ Interface[Long, String, _]) ~>
(Interface[Int, Int => String, _])
] =
Wiring(ba => a => ba._2, (ba, a) => (a, ba._1))
val r: Mealy[
(Store[Boolean, _]) ⊗ (Store[Boolean, _]) ~>
(Interface[Int, Long, _] ⊗ Interface[Long, String, _]) ~>
Interface[Int, Int => String, _]
] =
m.andThen(w).asMealy
val l: List[String] =
List(1, 2, 3, 4).mapAccumulate(r.init)(r.run)._2
// List("false", "false", "false", "true")Swap, Project, Discard, Duplicate
It is because Poly is a cartesian closed category that we can shuffle around types when defining our interfaces. Specifically, we have available to us an implicit set of operations familiar to most programmers: swap, project, discard, and duplicate. Together with the tensor product, they allow us to specify many wiring patterns, such as feedback systems, as well as dependently wired systems.
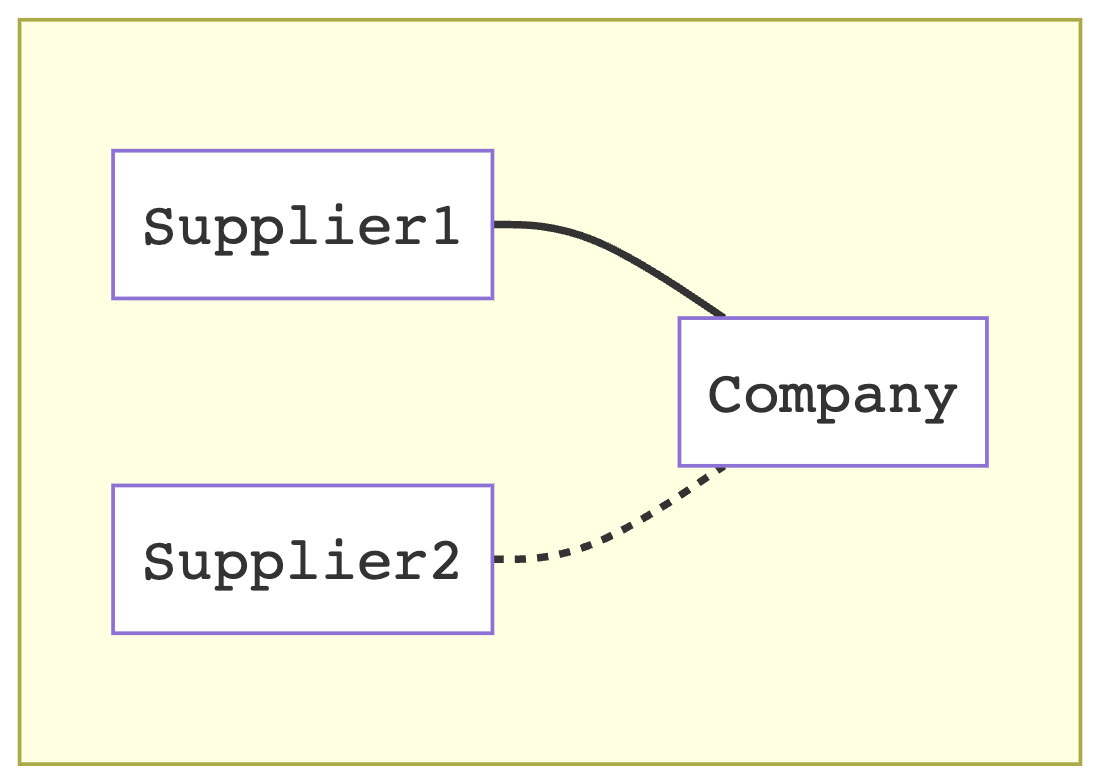
Dependent Systems
We can discard values and/or use them conditionally, based on system output. In effect, we can vary which wires are "connected" at a given state. In the following example, a company switches suppliers based on current stock:
type Supplier1[Y] = Monomial.Interface[Unit, Int, Y]
type Supplier2[Y] = Monomial.Interface[Unit, Int, Y]
type Company[Y] = Monomial.Interface[Int, Boolean, Y]
type System[Y] = Monomial.Interface[Unit, Unit => Boolean, Y]
type ω[Y] = ((Company ⊗ Supplier1 ⊗ Supplier2) ~> System)[Y]
val w: Wiring[ω] =
Wiring(
b => a => b._1._1, // emit status indicator
(b, a) => // if indicator is off, use supplier 1
((if b._1._1 then b._2 else b._1._2, a), a)
)
val m1: Moore[Monomial.Store[Int, _] ~> Company] =
Moore(
0,
s => if s > 2 then true else false, // indicate if stock exceeds 2
(s, i) => s + i // always accumulate state
)
val m2: Moore[Monomial.Store[Unit, _] ~> Supplier1] =
Moore((), _ => 1, (s, _) => s) // emit 1s
val m3: Moore[Monomial.Store[Unit, _] ~> Supplier2] =
Moore((), _ => 0, (s, _) => s) // emit 0s
val mealy: Mealy[
(Monomial.Store[Int, _] ⊗ Monomial.Store[Unit, _] ⊗ Monomial.Store[Unit, _]) ~>
(Company ⊗ Supplier1 ⊗ Supplier2) ~> System
] =
(m1 ⊗ m2 ⊗ m3).andThen(w).asMealy
val l: List[Boolean] =
List((), (), () ,()).mapAccumulate(mealy.init)(mealy.run)._2
// List(false, false, false, true)Feedback Systems
We can also define, as types, wiring diagrams that can only be implemented by sending output back as input, allowing us to model feedback within a dynamical system:
type Plant[Y] = Interface[(Byte, Byte => Char), Char, Y]
type Controller[Y] = Interface[Char, Byte => Char, Y]
type System[Y] = Interface[Byte, Byte => Char, Y]
type ω[Y] = ((Plant ⊗ Controller) ~> System)[Y]
val f1: Byte => Char = b => b.toChar
val f2: Byte => Char = b => b.toChar.toUpper
val m1: Moore[Store[Char, _] ~> Plant] =
Moore(
" ".charAt(0), // start with empty Char
c => c, // emit chars
(s, i) => i._2(i._1) // always apply the function passed
)
val m2: Moore[Store[Byte => Char, _] ~> Controller] =
Moore(
f1, // start with function 1
f => f, // emit function
(f, i) => if i != ' ' then f else f2 // switch function on ' '
)
val w: Wiring[ω] =
Wiring(
b => a => b._2(a), // readout to system
(b, a) => ((a, b._2), b._2(a)) // update to system
)
val machine: Mealy[
((Store[Char, _] ⊗ Store[Byte => Char, _]) ~>
(Plant ⊗ Controller) ~>
System)
] =
(m1 ⊗ m2).andThen(w).asMealy
val l: String =
"hello world".getBytes().toList.mapAccumulate(machine.init)(machine.run)._2.mkString
// "hello WORLD"So, as we can see, even single-mode, monomial lenses can exhibit complex and varying behaviors. But it also raises the question: what else does Poly put into reach?