Blog - Polynomial ADTs & Moore

Background

Every category has its objects and its morphisms. The category of Poly consists of polynomial functors, and natural transformations from one polynomial functor to another.

Objects

The objects of Poly are polynomial functors. What's a polynomial functor? "... an arbitrary coproduct of representables". In Scala, we can model them using familiar algebraic data types (ADTs). How so?

The claim is that "Poly categorifies highschool math". If by "algebraic" we mean cardinality and the counting of values, and we do, then:

An example provided in Haskell, y³ + y² + 2: data Foo y = Bar y y y | Baz y y | Qux | Quux
In Scala, we find cats.data.Representable, and we can identify the method def index[A](f: F[A]): Representation => A as a function that returns an exponential: A^{Representation}, i.e., in polynomial format of A => y, the term y^A.
And when we look at the example of cats.data.RepresentableStore we can see that type Store[S, A] = RepresentableStore[S => *, S, A] thus appears as a special case where both the functor and its indexing function are the same function, S => A, i.e., y^S. Yet, note that neither coproducts nor Store themselves form a Representable (e.g., gist), and rather, as a sum of representables, Store is a sum of an S number of representables S => A, i.e., S * (S => A), or, Sy^S.

So we can see how an ADT can be considered as a polynomial functor, for example, By^A:

sealed trait MyPolynomial[Y]
case class MyMonomial[A,B,Y](variable: A => Y, coefficient: B) extends MyPolynomial[Y]

And notably, we have the initial and terminal objects:

type `0`[Y] = MyMonomial[Nothing, Nothing, Y]
type `1`[Y] = MyMonomial[Unit, Nothing, Y]

Morphisms

"You'd never see, in highschool, arrows between polynomials, but they make sense". If the morphisms of Poly are maps from one polynomial functor to another, i.e., natural transformations, then can we model them in Scala? Yes, and no:

On one hand, given types P[_] and Q[_], then, thanks to Scala 3's polymorphic function types, it has never been easier to define a natural transformation val η: P ~> Q.
On the other hand, natural transformations in the full category of Poly are "dependent lenses", with P ~> Q being "computed by Yoneda and the universal mapping-out property of coproducts". In other words, we'll need dependent functions in order to implement any natural transformation that is not a map between monomials.
In a future post we will explore some strategies for modelling the full range of polynomial morphisms in Scala 3. This post will focus on what we can implement with simple types: the full subcategory of Poly spanned by the monomials, a.k.a Jules Hedges' "bimorphic lenses".

The key to defining maps between polynomials is the pair of "view" and "update" functions, φ and φ#, required to implement their natural transformation. For example, take the two monomials mentioned above, cats.data.RepresentableStore (let's call it Store) and MyMonomial:

 /* Monomials p and q */
case class Store[S, Y](peek: S => Y, index: S)                   // Sy^S
case class MyMonomial[A, B, Y](variable: A => Y, coefficient: B) // By^A

/* A type alias, for natural transformations between p and q */
type ~>[F[_], G[_]] = [Y] =>> F[Y] => G[Y]

/* A "view" function, derived from the coefficients of p and q */
def φ: S => B

/* An "update" function, derived from the exponents of p and q */
def `φ#`: (S, A) => S

/* A natural transformation from p to q, formed by φ and φ# */
def η[S, A, B]: ([Y] =>> Store[S, Y]) ~> ([Y] =>> MyMonomial[A, B, Y]) =
  [Y] =>
    (store: Store[S, Y]) =>
      MyMonomial[A, B, Y](
        `φ#`.curried(store.index).andThen(store.peek),
        φ(store.index)
      )

Forgive the clunky type lambdas. In the polynomial morphism above, mapping one monomial to another, we can make use of the following observations:

The pair of view and update functions completely specify the data of the natural transformation.
The polynomial that forms the codomain of the natural transformation can be said to "wrap" the polynomial that forms its domain.

In other words, monomial and polynomial morphisms are, respectively, simple and dependent lenses. And with type signatures like def ω: S𝑦^S → B𝑦^A, we can begin to see how to describe compositional state machines in the familiar language of polynomials. We'll be investigating the rich structure and the operations that this gives us access to.

Example: fs2 Stream Transducer

Let's look at polynomial functors in practice, beginning with the monomials: state lenses, wrappers, and wiring diagrams.

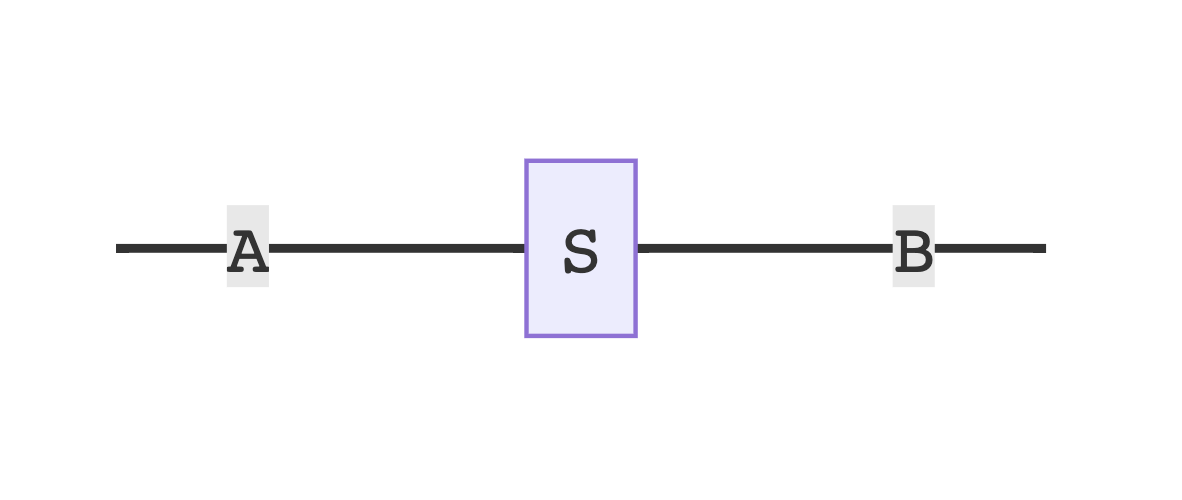
figure adapted from the poly book: state lens Sy^S ~> By^A. — A state machine lens: S𝑦^S → B𝑦^A.

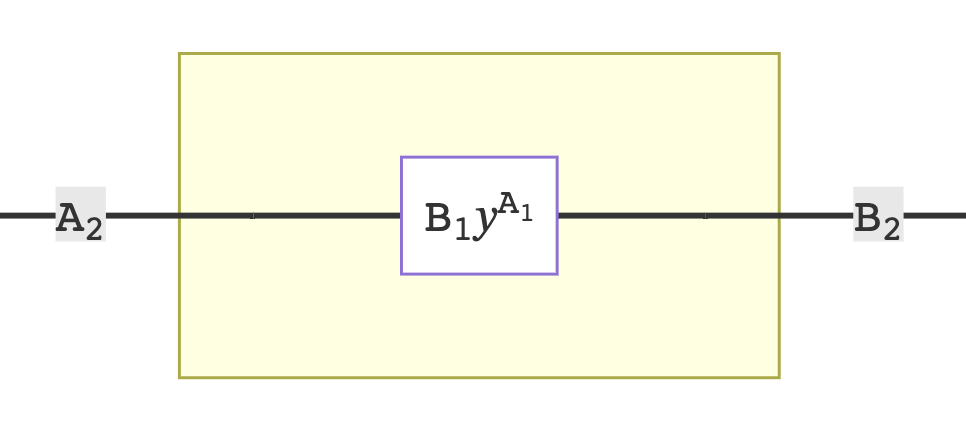
figure adapted from the poly book: interface lens By^A ~> By^A. — A wiring diagram lens: B₁𝑦^A₁ → B₂𝑦^A₂.

AB-Moore Machines

A poly map can model a Moore Machine. How so? Compare the above poly map between Store[S, Y] and MyMonomial[A, B, Y] to the definition of an AB-Moore machine, Moore[S, A, B], and note the similarity:

/* A "view" function */
def φ: S => B

/* An "update" function */
def `φ#`: (S, A) => S

Methods defining a poly map `Store → Interface`.

/* A "view" function */
def get: S => B

/* An "update" function */
def put: (S, A) => S

/* An "initial value" function */
def init: S

Methods defining an AB-Moore Machine.

As we build bigger and more complex machines, we'll see that Moore machines compose nicely and have their role. However there is one feature that a Moore machine lacks: a run function. And, for that, we turn to Mealy machines.

AB-Mealy Machines

A poly map can also model a Mealy Machine. An AB-Mealy Machine is essentially a Moore machine with a run function, i.e., an AB^A-Moore Machine. That is, given a value of the state, the machine outputs a "B", but the "B" is a function A => B, so that type Mealy[S, A, B] = Moore[S, A, A => B]. This let's us implement a run function, forming a finite state machine ideal for stream processing. Note the similarity between the run function and the argument to the mapAccumulate function as we'd find in cats or fs2:

/* A "view" function */
def φ: S => A => B

/* An "update" function */
def `φ#`: (S, A) => S

/* A "run" function */
def run: (S, A) => (S, B) =
    (s, a) =>
      (`φ#`(s, a), φ(s)(a))

Methods defining an AB-Mealy Machine.

/* A stream transducer function */
  def transducer[F[_], S, A, B](
    fsm: Moore[S, A, A => B]
  ): fs2.Stream[F, A] => fs2.Stream[F, B] =
    stream =>
      stream
        .mapAccumulate(fsm.init)(
          (s, a) =>
            (fsm.put(s, a), fsm.get(s)(a)))
        .map(_._2)

Methods defining an fs2 Stream transducer.

So, starting from two data types, Store[S, Y] and MyMonomial[A, B, Y], we've arrived at a simple state machine with a standardized run function. From this we can conclude:

Simple types are sufficient for modeling maps between monomials, and the state machines they represent.
Given a state, S, and an interface, referred to here as A ‒⛶→ B, we can form a map from one to the other, yielding a dynamical system A ‒🅂→ B.
View and update functions, and their types, are derived mechanically from the two functors, in a manner specified by the natural transformation of the two functors.

Once the init, readout, and update functions are provided, and a behavior of the state machine is thereby defined, then we have a Mealy machine, ready to process data:

val m: Moore[Monomial.Store[Boolean, _] ~> Monomial.Interface[Int, Int => Int, _]] =
  Moore[Boolean, Int, Int => Int, Y](
    false,
    s => x => if s then x + x else x,   // if we've seen x > 1, then emit 2x
    (s, x) => if x > 1 then true else s // change state upon seeing x > 1
  )

val n: Mealy[Monomial.Store[Boolean, _] ~> Monomial.Interface[Int, Int => Int, _]] 
  m.asMealy

val l: List[Int] =
  List(1, 2, 3).mapAccumulate(n.init)(n.run)._2
// l: List[Int] = List(1, 2, 6)

Defining and running a monomial state lens, a.k.a, a Mealy machine. A runnable example is available on GitHub.

Wiring Diagrams

Sometimes we care only about wires. That is, the interaction patterns alone, with the stateful components abstracted away, to be composed at a later step.

In the polynomial maps discussed so far, we've seen that if given a state, S, and an interface, referred to here as A ‒⛶→ B, we can form a map from one to the other, yielding a dynamical system A ‒🅂→ B. But poly maps can also represent wiring diagrams and enclosures, like -[‒A‒⛶‒B‒]-, where there is a "hole" for the state lens, and each box is an interface.

When a wiring diagram is composed with a state system, the outermost interface of the composite lens is called the "wrapper interface", where it serves as an adaptor to modify the state lens:

extension [S, A1, B1, Y] (p: (Store[S, _] ~> Interface[A1, B1, _])[Y])
  def andThen[A2, B2](
    w: (Interface[A1, B1, _] ~> Interface[A2, B2, _])[Y]
  ): (Store[S, _] ~> Interface[A1, B1, _] ~> Interface[A2, B2, _], _])[Y] =
    new (Store[S, _] ~>  Interface[A1, B1, _] ~> Interface[A2, B2, _])[Y]:
      def φ: PolyMap.Phi[Store[S, _] ~>  Interface[A1, B1, _], Interface[A2, B2, _], Y] =
        p.φ.andThen(w.φ)
      def `φ#`: PolyMap.PhiSharp[Store[S, _] ~>  Interface[A1, B1, _], Interface[A2, B2, _], Y] =
        (s, a) => p.`φ#`(s, w.`φ#`(p.φ(s), a))

Defining a lens composition for monomial lenses. Adapted from code available on GitHub.

We should quickly note some points about using Scala's simple types instead of fully dependent types:

We incur some library boilerplate by using simple types instead of dependent types.
We use match types Phi and PhiSharp for three purposes: to mitigate boilerplate, to derive function types, and to abstract over arity.
Hidden there in the Greek is the familiar, loopy, "there and back" implementation of lens composition.

But the main point is that, through lens composition, we've used a wiring diagram to turn an unrunnable Moore machine into a runnable Mealy machine. Once we initialize it and provide view and update functions, then we're ready for data:

val l: Moore[Store[Boolean, _] ~> Interface[Int, Int, _]] =
  Moore(false, s => if s then 1 else 0, (s, i) => s)

val m: Mealy[Store[Boolean, _] ~> Interface[Int, Int, _] ~> Interface[Int, Int => Int, _]] =
  l.andThen(Wiring(i => j => j + j, (i1, i2) => i2)).asMealy

val l: List[Int] =
  List(1, 2, 3).mapAccumulate(m.init)((s, i) => m.run(s, i))._2
// List(2, 4, 6)

Lens composition, yielding a runnable composite lens. Code available on GitHub.

A satisfying result. But this is only the beginning, it seems. We'll end this post having seen only monomials and only the most basic lenses. In order to see all that Poly has to offer, we'll need to explore a little further, and see just how far we can get with Scala's simple types.

Polynomial ADTs & Moore

Table of Contents:

Introduction

Overview

Caveats and Goals